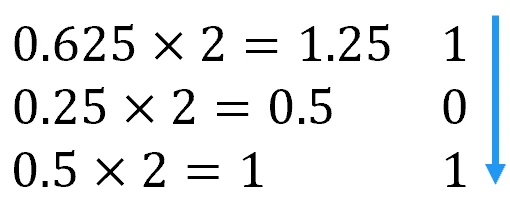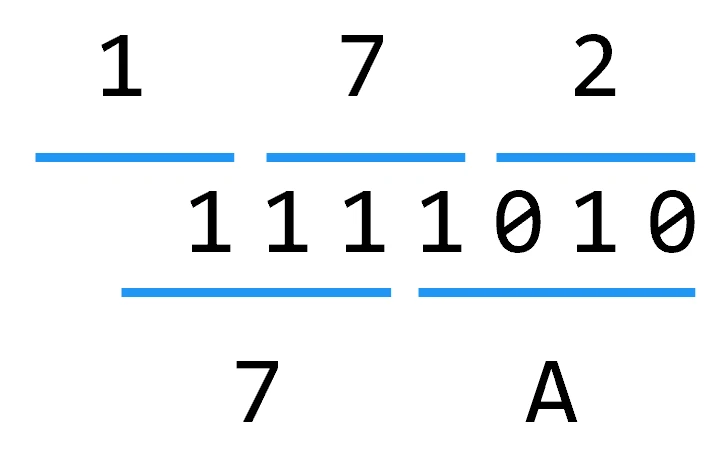数字类型

约 2796 个字 39 行代码 22 张图片预计阅读时间 10 分钟

本文包括进制、整数、浮点数、舍入方式、时间戳方面的知识，以及处理它们的注意事项。

基本概念

所有数据最终的存储形式是若干二进制位。

1 字节（Byte, B） = 8 位（bit）。

本内容讲解较为底层的概念，一些编程语言可能会对一些数据类型进行封装，故在占用空间等方面与本内容不符。

进制

概念

\(n\) 位整数，\(p\) 位小数的 \(m\) 进制的数，其转换为十进制的时候都有以下公式：

\[ \left(\overline{ABC\ldots N.abc\ldots l}\right)_m=Am^{n-1}+Bm^{n-2}+Cm^{n-3}+\ldots+Nm^0+am^{-1}+{bm}^{-2}+cm^{-3}+\ldots+lm^{-p} \]

常见的进制及其基数

二进制（binary, bin, b）
八进制（octal, oct, o）
十进制（decimal, dec, d）
十六进制（hexadecimal, hex, x）

十进制 ↔ 二进制

整数部分

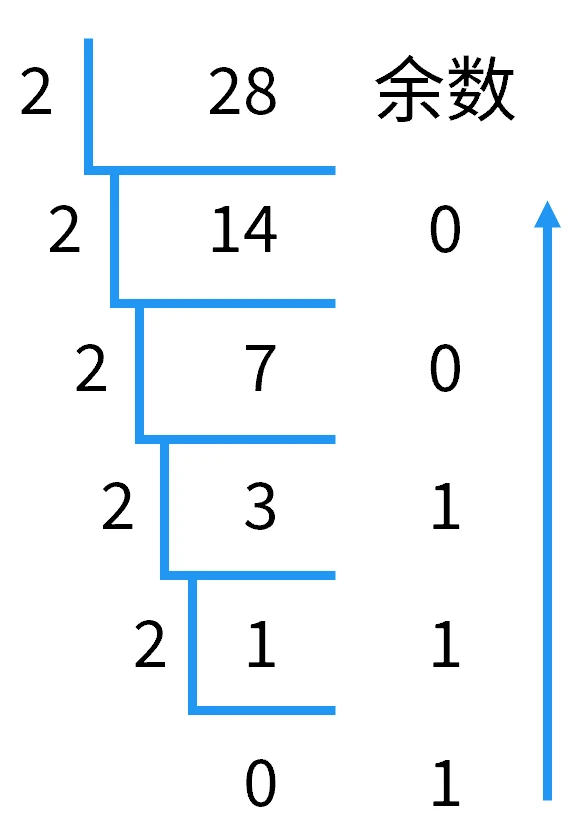
十进制转二进制

短除法，每次记余数，除到商为 0，向上读。

得 \(28=\left(11100\right)_2\)

二进制转十进制

使用之前的公式：

\[ {\left(11100\right)_2=1\times2^4+1\times2^3+1\times2^2+0\times2^1+0\times2^0\atop=16+8+4=28\ } \]

下面是 \(2^n\) 表格，方便快速计算：

n	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
\(2^n\)	1	2	4	8	16	32	64	128	256	512	1024	2048	4096	8192	16384	32768	65536

小数部分

十进制转二进制

乘 2，取整数部分，取到小数部分为 0 为止。

故 \(0.625=\left(0.101\right)_2\)

故 \(0.7=\left(0.1\dot{0}11\dot{0}\right)_2\)

进制转换可能出现除不尽的情况。

二进制转十进制

使用之前的公式：

\[ \left(0.101\right)_2=1\times2^{-1}+0\times2^{-2}+1\times2^{-3} =\frac{1}{2}+\frac{1}{8}=\frac{5}{8}=0.625 \]

二进制 ↔ 八进制、十六进制

八进制和十六进制是为了解决二进制数字太长而使用的。

二进制的三位构成八进制的一位，二进制的四位构成十六进制的一位。

故 \(\left(1111010\right)_2=\left(172\right)_8=\left(7A\right)_{16}\)

整数

Integer, int

辅助理解的工具 - 计算器

Windows 中的计算器切换到“程序员”模式，可以进行进制转换和位的显示。这里的整数都是有符号的。

名称	QWORD	DWORD	WORD	BYTE
位数	64	32	16	8
字节	8	4	2	1

整数的存储方式

以字节为单位，划分存储空间。故有取值范围。

如果有符号，最高位存储符号，0 正 1 负；余下的存储数值。

数值以数字转换为二进制后的结果的补码存储。

补码

非负数的补码为其自身。如 114：

如 01110010、0000000001110010

负数的补码为其绝对值的二进制结果取反加 1 的结果。如 -114：

绝对值 114 的二进制结果为 1110010
取反得 0001101
加 1 得 0001110
故其补码为 0001110
其存储形式

-114 的补码形式

如 10001110、1111111110001110

整数的取值范围

设 \(n\) 为存储的二进制位数

无符号整数的取值范围：\(0\ ~\ 2^n-1\)
带符号整数的取值范围： \({-2}^{n-1}\ ~\ 2^{n-1}-1\)

设 \(m\) 为存储的字节长度

无符号整数的取值范围：\(0\ ~\ 2^{8m}-1\)
带符号整数的取值范围：\({-2}^{8m-1}\ ~\ 2^{8m-1}-1\)

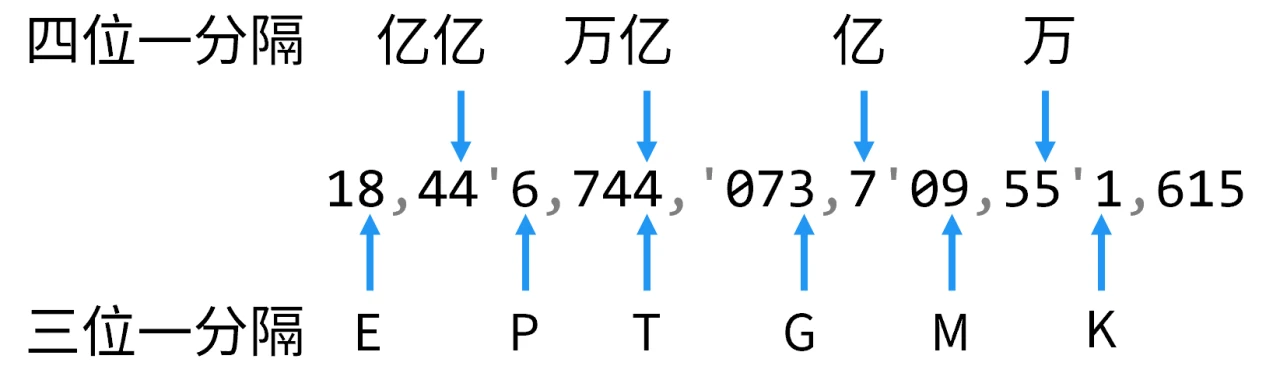
下面的表里面，数字位数过长。为方便理解，故用 , 按千位分隔，用 ' 按万位分隔。

字节数	1	2	4	8
位数	8	16	32	64
无符号上界	255	6'5,535	4,2'94,96'7,295	18,44'6,744,'073,7'09,55'1,615
带符号下界	-128	-3'2,768	-2,1'47,48'3,648	-9,22'3,372,'036,8'54,77'5,808
带符号上界	127	3'2,767	2,1'47,48'3,647	9,22'3,372,'036,8'54,77'5,807
C	`char`	`short`	`int`
C#	`sbyte`	`short`, `ushort`	`int`, `uint`	`long`, `ulong`
Java	`byte`	`short`	`int`	`long`
MySQL / MS SQL Server	`tinyint`	`smallint`	`int`	`bigint`

Python 的整数类型不采用底层的存储方式，故理论上无取值范围，取值范围与内存有关；只有带符号的
JS 只有浮点数 Number，没有内置的整数类型
斜体为无符号的数据类型；C、MySQL 通过在数据类型前加关键词 unsigned 来表示无符号类型

溢出

以带符号 8 位整数为例：

127：01111111；

加 1：10000000，为 -128

浮点数

float，计算机存储小数的方式。IEEE 754 规定了浮点数的存储方式。

浮点数的格式

可以类比科学计数法，如 \(-0.0000114=-1.14\times{10}^{-5}\)

\[ V=\left(-1\right)^SMR^E \]

其中：

\(V\) 为浮点数
\(S\) 为符号位（Sign），0 正 1 负
\(M\) 为尾数（Mantissa），以小数表示
\(R\) 为基数，整数，十进制为 10，二进制为 2
\(E\) 为指数（Exponent），整数

计算机中存储浮点数的格式

类比为 \(V=\left(-1\right)^S \times M \times 2^E\)

IEEE 754 规定的浮点数中，有两种浮点数比较常用：

名称	单精度浮点数（float）	双精度浮点数（double）
字节数	4	8
总位数	32	64
符号位 S 占位数	1	1
指数位 E 占位数	8	11
尾数 M 占位数	23	52

如果只提供一种浮点数类型，基本上就是双精度的（如 Python）。

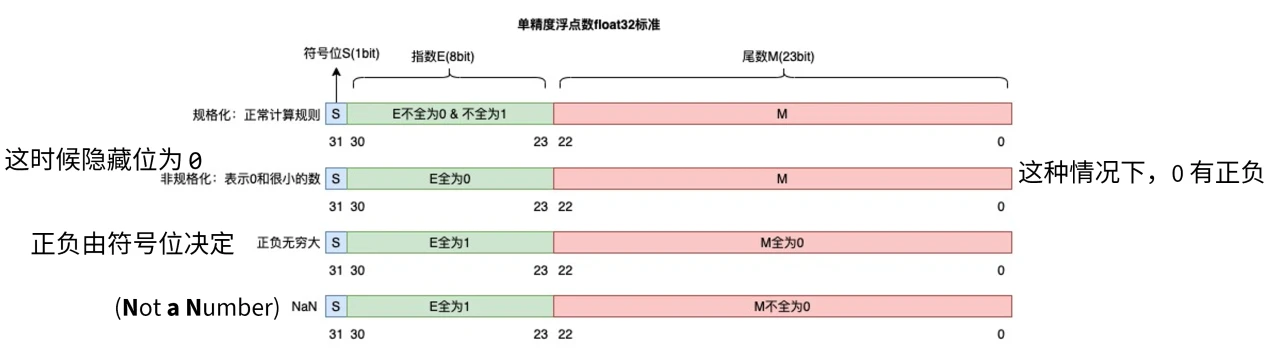
尾数和指数的特殊规定

尾数从高位开始存储。

尾数 \(M\) 默认以 1. 开头，但不需要体现在数据中，存储时存储其小数部分；故前面说的 1 这个开头被称为隐藏位。

指数 \(E\) 为无符号整数，但需要体现正负性，故存储时加上中间数：

单精度浮点数中间数为 127，取值范围 -127~128
双精度浮点数中间数为 1023，取值范围 -1023~1024

整个浮点数的特殊规定

取值范围

描述	指数	小数	单精度值	双精度值
0	`00…00`	`0…00`	0	0
1	`01…11`	`0…00`	1*2⁰ = 1	1*2⁰ = 1
最小非格式化数	`00…00`	`0…01`	2^-232^-126 = 1.410^-45	2^-522^-1022 = 4.910^-324
最大非格式化数	`00…00`	`1…11`	(1-ɛ)2^-126 = 1.210³⁸	(1-ɛ)2^-1022 = 2.210³⁰⁸
最小格式化数	`00…01`	`0…00`	12^-126 = 1.210^-38	12^-1022 = 2.210^-308
最大格式化数	`11…10`	`1…11`	(2-ɛ)2¹²⁷ = 3.410³⁸	(2-ɛ)2¹⁰²³ =1.810³⁰⁸

示例

25.125

整数部分 \(25=\left(11001\right)_2\)，小数部分 \(0.125=\left(0.001\right)_2\)

故 \(25.125=\left(11001.001\right)_2=\left(1.\ 1001001\right)_2\times2^4\)

则符号位 0，尾数 1001001；指数：

单精度：\(4+127=131=\left(10000011\right)_2\)
双精度：\(4+1023=1027=\left(10000000011\right)_2\)

因此，25.125 的浮点数存储形式为：

单精度：01000001110010010000000000000000
双精度：0100000000111001001000000000000000000000000000000000000000000000

-3.14

符号位 1；整数部分 \(3=\left(11\right)_2\)，小数部分 \(0.14=\left(0.0\dot{0}100011110101110000\dot{1}\right)_2\)

故 \(3.14=\left(11.0\dot{0}100011110101110000\dot{1}\right)_2=\left(1.10\dot{0}100011110101110000\dot{1}\right)_2\times2^1\)

则符号位 1，尾数 \(10\underline{1001000111101011100001}\cdots\)；指数：

单精度：\(1+127=128=\left(10000000\right)_2\)
双精度：\(1+1023=1024=\left(10000000000\right)_2\)

实际存储时，尾数超出位数部分要截断，会出现舍入的问题。截断的第一位为 0 则舍，为 1 则入：

因此，25.125 的浮点数存储形式为：

单精度：11000000010010001111010111000011
双精度：1100000000001001000111101011100001010001111010111000010100011111

该数的二进制为无限循环小数，且存在截断的舍入规则，故浮点数非准确值：

\[ \begin{align*} &\left(1.10010001111010111000011\right)_2\times2^{\left(10000000\right)_2-127} \\ &=\frac{2^{23}+2^{22}+2^{19}+2^{15}+2^{14}+2^{13}+2^{12}+2^{10}+2^8+2^7+2^6+2+1}{2^{23}}\times2 \\ &=3.1400001049041748046875 \\ \end{align*} \]

\[ \begin{align*} &\left(1.1001000111101011100001010001111010111000010100011111\right)_2\times2^{\left(10000000000\right)_2-1023} \\ &=3.1400000000000001243449787580175325274467468261718750 \\ \end{align*} \]

0.1 + 0.2 ≠ 0.3

\[ 0.1=\left(0.0\dot{0}01\dot{1}\right)_2=\left(1.\ \dot{1}00\dot{1}\right)_2\times2^{-4} \]

\[ 0.2=\left(0.\dot{0}01\dot{1}\right)_2=\left(1.\ \dot{1}00\dot{1}\right)_2\times2^{-3} \]

0.1 与 0.2 的指数不一样，相加时要左移 0.1 的小数点一位；注意隐藏位：

故 0.1 + 0.2 的浮点数运算结果：

单精度：0.300000011920928955078125
双精度：0.3000000000000000444089209850062616169452667236328125

因此在绝大多数语言中，0.1 + 0.2 ≠ 0.3。

各语言的执行结果可以参考 https://0.30000000000000004.com/。

类似的问题还有：

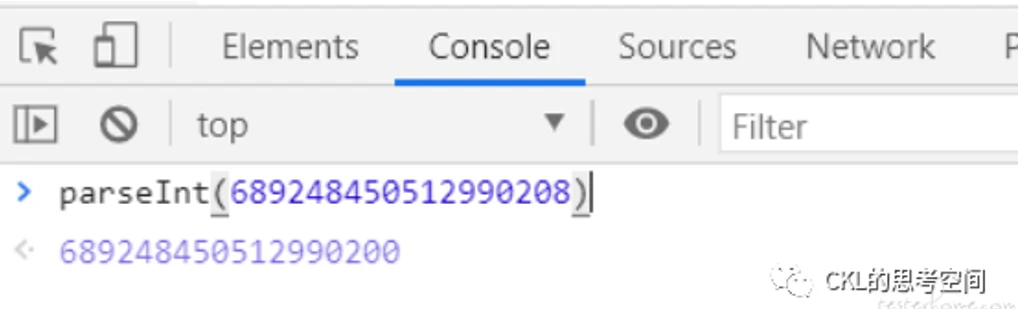
300.01 - 300 < 0.01
689248450512990208.0 == 689248450512990200.0

>>> 0.1 + 0.2
0.30000000000000004
>>> 300.01 - 300
0.009999999999990905
>>> 689248450512990208.0 == 689248450512990200.0
True

JS 只有浮点数类型，故较常遇到该问题。

或许可以通过保留小数位数的方法解决，但依然不稳定。

Excel 中的浮点数问题

身份证号、手机号必须强制以字符串存储（可在输入前加上英文引号 '），不能直接输入数字。

尤其是身份证号，如果以数字存储，会丢失后几位的信息，无法恢复。

判断一个浮点数是否为 `NaN`

据 IEEE 754，NaN 不应等于任何其他数值，包括自身。

在 Python 中，需要用 isnan() 函数判断一个浮点数是不是 NaN

较为精确的小数

Python 中的精确计算（标准库）

fractions.Fraction 类：表示分数
decimal.Decimal 类：表示若干位有效数字的十进制小数

`Fraction`

整数构成的分数，可以表示任意有理数。

可以通过整数、浮点数（不推荐）、字符串、Decimal 对象等构建。

>>> from fractions import Fraction
>>> Fraction(16, -10)
Fraction(-8, 5)
>>> Fraction(123)
Fraction(123, 1)
>>> Fraction(1.1)
Fraction(2476979795053773, 2251799813685248)    # 因此不推荐用浮点数构建
>>> Fraction('1.1')
Fraction(11, 10)
>>> Fraction('1/5')
Fraction(1, 5)

`Decimal`

给定有效数字的十进制小数。

可以通过整数、浮点数（不推荐）、字符串构建。

默认有效数字为 28，可更改。

>>> from decimal import Decimal, getcontext
>>> Decimal(1) / Decimal(7)
Decimal('0.1428571428571428571428571429')
>>> getcontext().prec = 128     # 更改有效数字位数
>>> Decimal(1) / Decimal(7)
Decimal('0.14285714285714285714285714285714285714285714285714285714285714285714285714285714285714285714285714285714285714285714285714285714')
>>> Decimal('0.1') + Decimal('0.2')
Decimal('0.3')
>>> Decimal(0.1) + Decimal(0.2)
Decimal('0.3000000000000000166533453693773481063544750213623046875')    # 因此不推荐用浮点数构建

四则运算等和其他的无异。

一些数学函数要使用 Decimal 对象的方法，不能使用 math 库。

>>> Decimal(2).sqrt()
Decimal('1.414213562373095048801688724')

其他方式

其他语言和系统中类似的部分：

Java 的 BigDecimal 类（java.math.BigDecimal）
JS 使用 bignumber.js、decimal.js、big.js 第三方库
C# 使用 money 或 decimal 数据类型
MySQL 中有 decimal 类型
Microsoft SQL Server 有 numeric 类型

对于金额之类的有固定小数位数的，也可使用整数存储数值。如：阿里巴巴的 Java 开发手册中，强制要求金额使用最小货币单位存储整数。

数的舍入

IEEE 754 规定了 4 种舍入方式：

舍入方式	俗称	舍的情况	入的情况
就近舍入 / 向偶数舍入	四舍六入五取偶	<5; =5 且后位为偶	>5; =5 且后位为奇
朝 0 舍入	去尾	所有	无
朝正无穷舍入 / 向上舍入		负数，0	正数
朝负无穷舍入 / 向下舍入		正数，0	负数

舍入结果例：

舍入方式	1.4	1.5	1.6	2.5	-1.5
四舍五入	1	2	2	3	-2
就近舍入 / 向偶数舍入	1	2	2	2	-2
朝 0 舍入	1	1	1	2	-1
朝正无穷舍入 / 向上舍入	2	2	2	3	-1
朝负无穷舍入 / 向下舍入	1	1	1	2	-2

一般来说：

默认的舍入方式（round）都是就近舍入
向上舍入（ceil）
向下舍入（floor）
强制转换数据类型也是向下舍入

Python `Decimal` 对象的舍入方式

Decimal对象.quantize(标识小数位数的Decimal对象[, 舍入方式])

舍入方式（都是 Decimal 下的常量）：

ROUND_CEILING：总是趋向无穷大向上取整（朝正无穷舍入，向上舍入）
ROUND_DOWN：总是趋向 0 取整（朝 0 舍入，去尾）
ROUND_FLOOR：总是趋向负无穷大向下取整（朝负无穷舍入，向下舍入）
ROUND_HALF_DOWN：如果最后一个有效数字大于 5，则朝 0 反方向取整；否则，趋向 0 取整（默认）
ROUND_HALF_EVEN：类似于 ROUND_HALF_DOWN，不过，如果最后一个有效数字值为 5，则会检查前一位。偶数值会导致结果向下取整，奇数值导致结果向上取整（就近舍入，向偶数舍入，四舍六入五取偶）
ROUND_HALF_UP：类似于 ROUND_HALF_DOWN，不过如果最后一位有效数字为 5，值会朝 0 的反方向取整（四舍五入）
ROUND_UP：朝 0 的反方向取整（进一）
ROUND_05UP：如果最后一位是 0 或 5，则朝 0 的反方向取整；否则向 0 取整

>>> import decimal
decimal.Decimal('50.5679').quantize(decimal.Decimal('0.00'))
# decimal.Decimal('50.57')
>>> Decimal('2.5').quantize(Decimal('0'), ROUND_HALF_DOWN)
Decimal('2')
>>> Decimal('2.5').quantize(Decimal('0'), ROUND_HALF_UP)
Decimal('3')
>>> Decimal('2.5').quantize(Decimal('0'))
Decimal('2')

Excel 中的舍入问题

Excel 有 15 位有效数字，保存为 CSV 后只有 9 位。如果 CSV 文件中有有效位数多的小数，不要用 Excel 保存，会丧失小数位。

时间戳

定义

将某个特定的时间点记为 0 或 1，以某个时间单位为单位 1，累加 / 减的结果可以用来记录时间，视情况为带符号 / 无符号整数或浮点数。

绝大多数语言使用 POSIX 时间（一般称为 Unix 时间戳，一般说的时间戳即为此），将 UTC 时间 1970-01-01 00:00:00 记为 0，以 1 秒或 1 毫秒为单位 1。

UTC 时间一般来说相当于北京时间减 8 h，所以上述时间的北京时间为同日 8 时。

Excel 中，将 1900-01-01 00:00:00 记为 1，以 1 天为单位 1，不支持负数；小于 1 的时候会出现 1900-01-00 的情况。

2038 年问题

时间戳以带符号 32 位整数形式存储时：

2038-01-19 03:14:07 记为：01111111 11111111 11111111 11111111

再往后一秒，会造成溢出，结果为：10000000 00000000 00000000 00000000

即 1901-12-13 20:45:52

使用 64 位整数可以解决问题，将时间最大值扩展到 292,2'77,02'6,596-12-04 15:30:08

一般来说 32 位的软硬件设备会受该问题影响，64 位的不会。

数字类型

基本概念

进制

概念

常见的进制及其基数

十进制 ↔ 二进制

整数部分

十进制转二进制

二进制转十进制

小数部分

十进制转二进制

二进制转十进制

二进制 ↔ 八进制、十六进制

整数

辅助理解的工具 - 计算器

整数的存储方式

补码

整数的取值范围

溢出

浮点数

浮点数的格式

计算机中存储浮点数的格式

尾数和指数的特殊规定

整个浮点数的特殊规定

取值范围

示例

25.125

-3.14

0.1 + 0.2 ≠ 0.3

Excel 中的浮点数问题

判断一个浮点数是否为 NaN

较为精确的小数

Python 中的精确计算（标准库）

Fraction

Decimal

其他方式

数的舍入

Python Decimal 对象的舍入方式

Excel 中的舍入问题

时间戳

定义

2038 年问题

参考资料

判断一个浮点数是否为 `NaN`

`Fraction`

`Decimal`

Python `Decimal` 对象的舍入方式